type
status
date
summary
password
category
slug
icon
🌧️流密码(Stream cipher)
- 明文逐位与密钥流进行异或运算,生成密文流
- 又称序列密码
- 对称加密算法,加密和解密双方使用相同伪随机加密数据流(pseudo-random stream)作为密钥
- 流密码的安全性依赖于生成高质量的密钥流。
- 密钥流应该是伪随机的,不可预测的,并且对于同一个密钥,不应该重复出现。
流密码的分类
依据流密码密钥序列产生的方式,可以将流密码分为同步流密码和自同步流密码两类。
同步流密码:如果密钥流产生的算法和产生的密钥序列都与明文或密文无关,我们称这类流密码为同步流密码。
自同步流密码:密钥流产生的算法与明文相关,则所产生的密钥序列也与明文相关,称这类流密码为自同步流密码
同步流密码
同步流密码可以分为密钥流产生器和加密变换器两部分
在同步流密码中,前面出现的加解密错误不会影响到后面的加解密,这是因为相邻两位明文的加密是相互独立,没有关系的。
同步流密码在加密或解密时,需要使两者密钥流生成器的状态一致(这里的状态可以决定密钥流生成器产生的密钥),否则会导致加解密密钥不一致,使解密失败。当两者密钥流生成器的状态不一致时,必须借助外接手段来同步,同步流密码本身不具有自同步功能,FB、CTR模式就属于同步流密码
自同步流密码
密钥产生算法是密钥和以往密文序列的函数,则称这种流密码为自同步流密码。
自同步流密码中,密钥序列的产生与明文的加密是不独立的,也是不能分割的。很多情况下,明文或者密文都需要给密钥序列的产生提供反馈。
自同步流密码具有自同步功能。因为密钥序列的产生与明密文序列有关,所以加密和解密密钥生成器的状态不一致时,是可以自己进行同步的,无需认为同步。
自同步流密码可能会对错误进行传播。因为密钥序列的产生与明文序列有关,所以前边明文的加密错误,会导致后边密钥序列生成出错,导致后边明文序列也加密错误。
CFB模式就属于同步流密码
二元加法流密码
一种基于二进制加法运算的流密码算法。它使用一个密钥流和明文流进行逐位的二进制加法运算,生成密文流

一次一密(one-time pad)
- 又称Vernam加密法
- 将明文与随机生成的密钥进行异或运算来实现加密和解密
- 密钥:与明文等长、完全随机、只使用一次,并且发送者和接收者在事先共享同一密钥。
- 不能提供完整性验证和认证
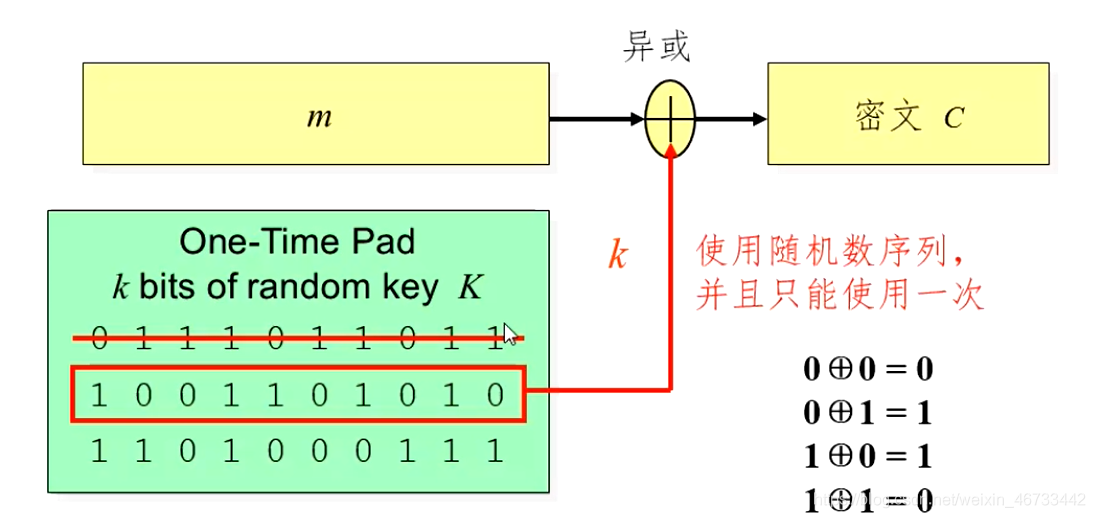
一次一密的密钥长度和明文一样长,流密码不是,需要种子密钥通过密钥生成器产生密钥流
多次一密(Many Time Pad Attack)
多次一密攻击的关键在于密钥重复使用。由于密钥序列在多次加密中重复使用,攻击者可以通过异或运算的性质,推断出密钥流的一部分或全部内容,从而破解密钥和解密密文。
异或运算性质
这个攻击的原理是 ,而通过 可以分析出 ,因此 不再安全。
两个密文的异或,就等于对应明文的异或,可以通过频率分析,来破译这些密文。
ascii表
ascii 码表在 Linux 下可以通过
man ascii 指令查看。它的性质有:0x20是空格。 低于0x20的,全部是起特殊用途的字符;0x20~0x7E的,是可打印字符。
0x30~0x39是数字0,1,2...9。
0x41~0x5A是大写字母A-Z;0x61~0x7A是小写字母a-z
小写字母 ⊕ 空格,会得到对应的大写字母;大写字母 ⊕ 空格,会得到小写字母!所以,如果x ⊕ y得到一个英文字母,那么中的某一个有很大概率是空格
例题--[AFCTF2018]你听过一次一密么?
题目
攻击击过程显而易见:对于每一条密文c1,拿去异或其他所有密文。然后去数每一列有多少个英文字符,作为c1在这一位是空格的评分。
上面的事情做完时候,依据评分从大到小排序,依次利用 “某个明文的某一位是空格” 这种信息恢复出所有明文的那一列。如果产生冲突,则舍弃掉评分小的。
脚本:
🔑伪随机密钥流
伪随机序列
伪随机序列也就是,即使截获其中一段,也无法推测后面是什么。(只能要求截获比周期短的一段密钥流时不会泄露更多信息, 这样的序列称为伪随机序列。)
伪随机数生成器
🪄线性同余生成器 / 线性同余方法(LCG)
线性同余方法(LCG)是个产生伪随机数的方法
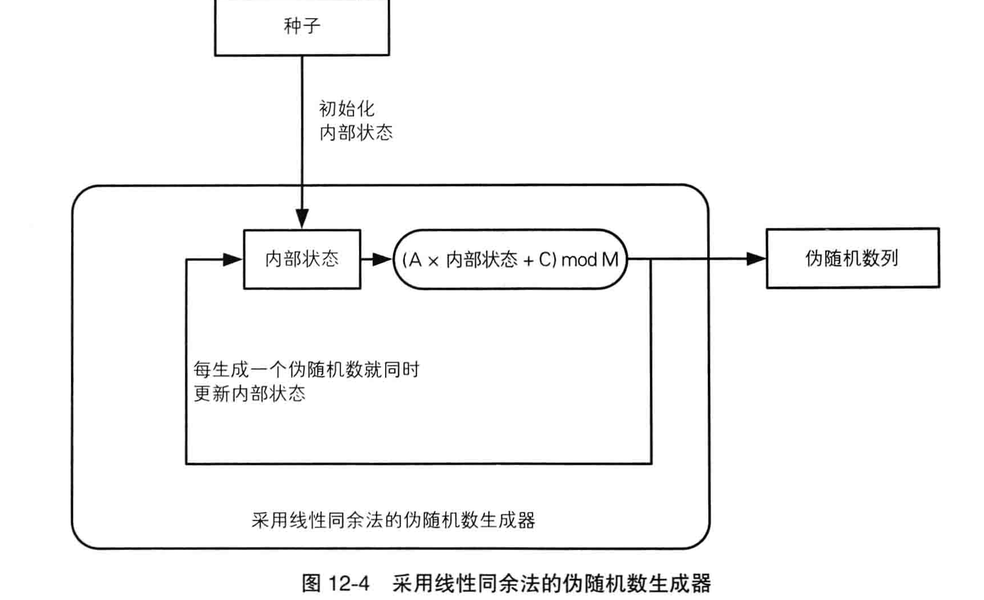
LCG的性能和随机性取决于选取的参数。如果选择恰当的参数,LCG可以生成长周期和均匀分布的伪随机数序列。然而,不恰当的参数选择可能导致序列的周期较短或者存在可预测的模式,从而影响其随机性和安全性
LCG的周期最大为 M,但大部分情况都会少于 M。要令LCG达到最大周期,应符合以下条件:
- B,M 互质;
- M 的所有质因数都能整除 A-1;
- 若 M 是4的倍数,A-1也是;
- A,B,N0都比 M 小;
- A,B是正整数。
🪄线性反馈移位寄存器(Linear Feedback Shift Register,简称LFSR)
用于生成一个伪随机的比特序列,常用于加密、编码、通信等领域。
移位寄存器是流密码产生密钥流的一个主要组成部分,GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数组成。
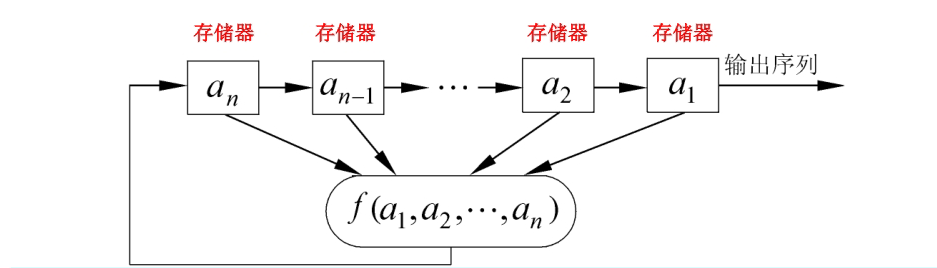
移位寄存器三要素:
- 初始状态:由用户确定
- 反馈函数: 是 n元布尔函数,即函数的自变量和因变量只取0和1这两个可能值(题目给出)
- 输出序列

对于 $n$ 级线性反馈移位寄存器
- 最长周期为 $2^n-1$(排除全0),达到最长周期的序列一般称为 $m$ 序列。
- 完全由其反馈函数决定。
- n级LFSR状态数:最多有2^n个
- 输出序列的周期 = 状态周期 <= 2^n - 1
🪄🪄MT19937(梅森旋转算法(Mersenne Twister Algorithm,简称 MT))
为了解决过去伪随机数发生器(Pseudo-Random Number Generator,简称 PRNG)产生的伪随机数质量不高而提出的新算法。常见的两种为基于32位的 MT19937和基于64位的 MT19937-64。
由于梅森旋转算法是利用**线性反馈移位寄存器(LFSR)**产生随机数的,对于LFRS有结论:一个 k 位的移位寄存器,选取合适的特征多项式(即加1为本原多项式)时,取得最大周期 $2^k-1$.
而MT19937梅森旋转算法的周期为$ 2^{19937}−1$ (正如算法名,这是一个梅森素数),说明它是一个19937级的线性反馈移位寄存器,梅森旋转算法是利用线性反馈寄存器一直进行移位旋转,因此实际上 MT19937-32只需要用32位就能做到。它能做到在 $1≤k≤623 $都可以均匀分布。
Mersenne Twister 最常见的实现方式使用 624 个 32 bits 的初始状态。这些整数按顺序分发(分发前对每个初始数进行转换),分发完后对该状态应用某种算法以获取下一组 624 个整数。以及可以通过得到连续的 624 个输出,还原出原来的 624 个 states,再根据原算法推算出接下来每个 state 下一次的 value,从而算出接下来的输出
算法
整个算法主要分为三个阶段:
- 第一阶段:获得基础的梅森旋转链;
- 第二阶段:对于旋转链进行旋转算法;
- 第三阶段:对于旋转算法所得的结果进行处理;
第一阶段
导入seed,初始化伪随机数发生器
使用一个循环从索引1到623的范围,为
mt 列表的其他元素赋值。赋值的方式基于 Mersenne Twister 算法的核心公式。_int32()是一个辅助函数,用于确保结果是32位有符号整数。
(self.mt[i - 1] ^ self.mt[i - 1] >> 30)表示对mt列表中前一个元素进行右移30位的操作,然后与前一个元素进行异或运算。
1812433253是一个常数。
+ i表示将索引值加到结果中,以产生不同的种子序列。
第二阶段
进行
twist() 函数==
twist() 方法==用于对生成器的状态进行旋转操作。它的操作步骤如下:- 使用一个循环从索引0到623的范围,依次处理每个状态元素。
- 根据状态元素的索引,获取当前元素和下一个元素的值。
- 对获取的值进行位操作,包括按位与和按位异或,以改变当前元素的值。(
(self.mt[i] & 0x80000000)获取当前元素的最高位,(self.mt[(i + 1) % 624] & 0x7fffffff)获取下一个元素的其余31位。这样可以将当前元素的最高位和下一个元素的其余31位合并成一个32位的值。将获取的值存储到变量y中,并使用_int32()函数将其转换为32位有符号整数。对当前元素进行状态扭曲操作。首先,使用右移运算符将y的值向右移动1位,然后与索引为(i + 397) % 624的状态元素进行按位异或运算。如果y的值除以2的余数不为0,即y % 2 != 0,则将当前元素与常数0x9908b0df进行按位异或运算。)
- 将结果存储回
mt列表的当前元素位置。
第三阶段
==
extract_number() 方法==用于从生成器中提取一个伪随机数。它的操作步骤如下:- 首先,检查
mti(mti 是用于追踪 mt 列表中当前使用的元素的索引) 是否等于0,如果等于0,则调用twist()方法进行状态的扭曲操作,以生成新的伪随机数序列。
- 接下来,从
mt列表中获取当前的随机数,存储到变量y中。
- 对
y执行一系列的位运算操作,包括右移、异或、左移和按位与,以改变y的值。
- 更新
mti的值,将其加1并对624取模,以确保它在0到623之间循环。
- 返回
_int32(y),其中_int32()是一个辅助函数,用于确保结果是32位有符号整数。
实现
使用MT19937算法生成范围在 [232−1]
的均匀分布的32位整数。
破解
右移位后异或逆向
左移位后异或逆向
提取伪随机数逆向
通过输出参数逆向
完整代码
常见流密码
RC4
- RC4由伪随机数生成器和异或运算组成。
- RC4的密钥长度可变,范围是[1,255]。
- RC4一个字节一个字节地加解密。
- 给定一个密钥,伪随机数生成器接受密钥并产生一个S盒。S盒用来加密数据,而且在加密过程中S盒会变化。
- 由于异或运算的对合性,RC4加密解密使用同一套算法。
RC4产生非线性的密钥流序列,先密钥调度算法初始化S表,再伪随机生成算法修改S表选取随机元素作为k
密钥调度算法
- 对S表线性填充,. S盒(0-255)
- 种子密钥重复填充K表,K(0)=1,K(1)=2,K(3)=3,K(4)=1,K(5)=2,⋯ ⋯( K 表只有(1,模))